√ y=x^2 2x-8 in vertex form 296628-Y=x^2+2x-8 in vertex form

Answer by dfrazzetto (2) ( Show Source ) You can put this solution on YOUR website!Satandard form factored form vertex form any form ***** MATH 45Divide 22\sqrt {y} by 2 The equation is now solved Swap sides so that all variable terms are on the left hand side Factor x^ {2}2x1 In general, when x^ {2}bxc is a perfect square, it can always be factored as \left (x\frac {b} {2}\right)^ {2} Take the square root of

Draw The Graph Of The Polynomial F X X 2 2x 8

Y=x^2+2x-8 in vertex form

Y=x^2+2x-8 in vertex form-When graphing the parabola in standard form, to find the vertex we use the following method The xvalue of the vertex is calculated as x = b/(2a) The yvalue of the vertex is f(b/(2a)) The xvalue of the vertex also represents the horizontal shift, while the y Find an answer to your question Write the function in vertex form y=x^26x3 BruhhItsCaroline BruhhItsCaroline Mathematics Middle School answered Write the function in vertex form y=x^26x3 2 See answers znk znk Answer y = 1(x 3)²

Www Scasd Org Cms Lib Pa Centricity Domain 1229 2 2 a2 17 unit 2 2 ws packet lg Pdf

 The equation in vertex form is By looking at the equation we can understand that the y value of the vertex point is 6 By further calculation we can verify that the x value of the vertex point is 3 Now, there are two ways of finding if the vertex point is a maximum or a minimum The first way is picking random x coordinates after andThe axis of symmetry and the vertex of this quadratic function are calculated by hand The results are compared with the results obtained by using a graphing1) y=(x−17)(x2) 2)y=(x−17)(x−2) 3)y=(x−6)2 2 4) y=(x−6)2 −2 6 Which equation and ordered pair represent the correct vertex form and vertex for j(x) =x2 −12x7?

Learn to complete the square in order to write quadratic equations in vertex form Click Create Assignment to assign this modality to your LMS We have a new and improved read on this topicSolving x 22x8 = 0 directly Earlier we factored this polynomial by splitting the middle term let us now solve the equation by Completing The Square and by using the Quadratic Formula Parabola, Finding the Vertex 31 Find the Vertex of y = x 22x8 Parabolas have a highest or a lowest point called the Vertex Vertex Form Of A Quadratic The vertex form of a quadratic is given by y = a(x – h) 2 k, where (h, k) is the vertexThe "a" in the vertex form is the same "a" as in y = ax 2 bx c (that is, both a's have exactly the same value) The sign on "a" tells you whether the quadratic opens up or opens downThink of it this way A positive "a" draws a smiley, and a negative

My initial idea was to take the derivative, and set it to zero y = x^2 8x 10 dy/dx = 2x 8 Setting that to zero gives an x value of 4, and plugging x = 4 into the first equation gives y = 6 Thus, the veQuestion Write y=2x^212x14 in vertex form Answer by jim_thompson5910 () ( Show Source ) You can put this solution on YOUR website!Y = (x 2 2x 8) y = (x 2 2x 8) y = (x 2 2 ⋅ x ⋅1 1 218) y = ((x1) 29) y = (x1) 2 9 By comparing this with the vertex form of parabola, we get (h, k) ==> (1, 9) Example 6 y = (x1)(x3) Solution y = x 24x3 y = x 22 ⋅ x ⋅2 2 22 2 3 y = (x2) 243 y = (x2) 21

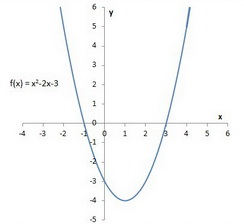
How Do I Convert The Equation F X X 2 2x 3 To Vertex Form Socratic

3 Vertex Form

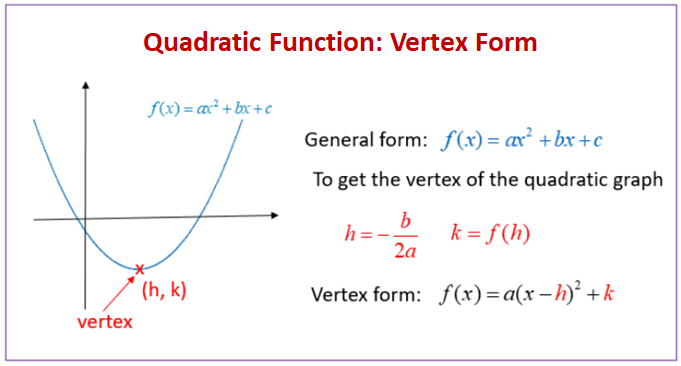
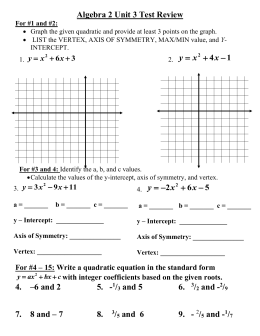
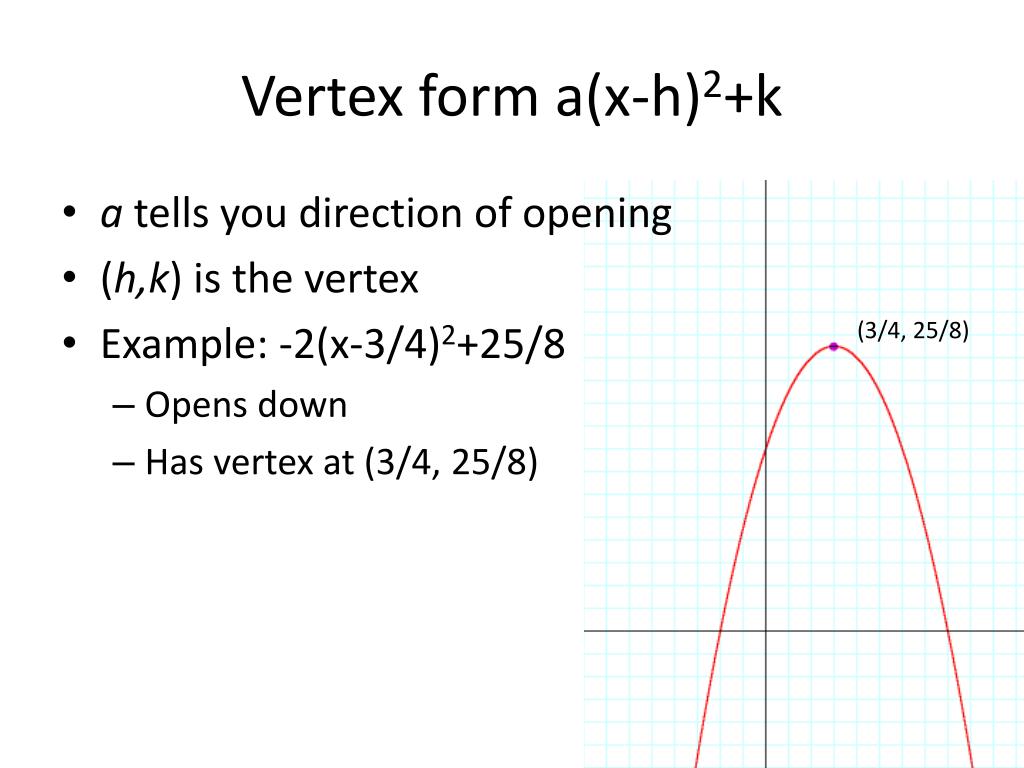
The vertex form is a special form of a quadratic function From the vertex form, it is easily visible where the maximum or minimum point (the vertex) of the parabola is The number in brackets gives (trouble spot up to the sign!) the xcoordinate of the vertex, the number at the end of the form gives the ycoordinate This means If the vertex form is , then the vertex is at (hk) How to put a function into vertex form?While the standard quadratic form is a x 2 b x c = y, the vertex form of a quadratic equation is y = a ( x − h) 2 k In both forms, y is the y coordinate, x is the x coordinate, and a is the constant that tells you whether the parabola is facing up ( a) or down ( − a ) (I think about it as if the parabola was a bowl of applesauce The equation of a parabola in vertex form is ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯∣∣ ∣ 2 2y = a(x − h)2 k2 2 ∣∣ ∣ −−−−−−−−−−−−−−−−−−−−− where (h ,k) are the coordinates of the vertex and a is a constant Rearrange y = x2 − 2x into this form using the method of completing the square y = (x2 −2x1)−1 ⇒ y = (x −1)2 − 1 ← in vertex form

Solution What Is The Vertex Form Of F X X 2 2x 5

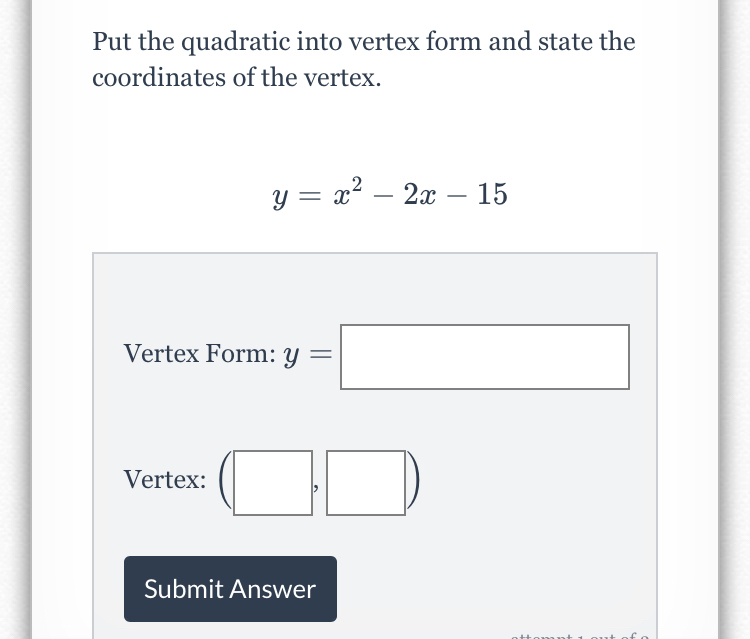
Answered Put The Quadratic Into Vertex Form And Bartleby

Answer by Edwin McCravy () ( Show Source ) You can put this solution on YOUR website!Write y=2x^24x12 in vertex form 1 See answer shuvt is waiting for your help Add your answer and earn points masonlawiii masonlawiii This is the answer y=2(x1)^28 nope apperently its y=2(x1)^210 New questions in Mathematics In exercise 5 Best Answer For the general quadratic equation \(y=ax^2bxc\) the vertex occurs where \(x_{vertex}=\frac{b}{2a}\) To find the value of y at that point, put this back into the quadratic equation \(y_{vertex}=(\frac{b}{2a})^2b(\frac{b}{2a})c\) In vertex form the quadratic can now be written as \(yy_{vertex}=(xx_{vertex})^2\) See if you can apply this to your

Write The Equation In Vertex Form Y X 2 2x 8 Study Com

How To Put An Equation Into Vertex Form Quora

1) write y=4x^232x66 in vertex form Complete the square y= 4x^32x64 66 64 y= (2x8)^2 2 vertex = 4,2 2)use the quadratic formula to solve the equation 4x^2x3=0A vertical stretch or compression a > 0, the parabola opens up and there is a minimum value a< 0, the parabola opens down and there is a maximum value (may also be referred to as a reflection in the xaxis) 1 y = x² 4x 12 When y = 0 x² 4x 12 = 0 x² 4x 12 = 0 (x 2)(x 6) = 0 x = 2 or x = 6 The xintercepts are 2 and 6 y = (x² 4x) 12 y = (x²

Why Is It In Vertex Form Of Quadratic Function Y A X H 2 K Getting Value Of H Is Opposite To Its Value Quora

3

 Method 1 Converting to Vertex Form Vertex form can be represented as #y=(xh)^2k# where the point #(h,k)# is the vertex To do that, we should complete the square #y=x^22x2# First, we should try to change the last number in a way so we can factor the entire thing #=># we should aim for #y=x^22x1# to make it look like #y=(x1)^2#Free Parabola Vertex calculator Calculate parabola vertex given equation stepbystep This website uses cookies to ensure you get the best experience Convert equation from quadratic form to vertex form, y= a(xh)^2 k, by completing the square y= 25x^255x525 Algebra For the given quadratic equation convert into vertex form, find the vertex, and find the value for x = 6

Writing Quadratic Equations From Vertex Form To Standard Form Practice Worksheet Quadratics Quadratic Equation Equations

The Vertex Form Of The Equation Of A Parabola Is Y 1 2 X 4 Squared 13 What Is The Standard Form Of Brainly Com

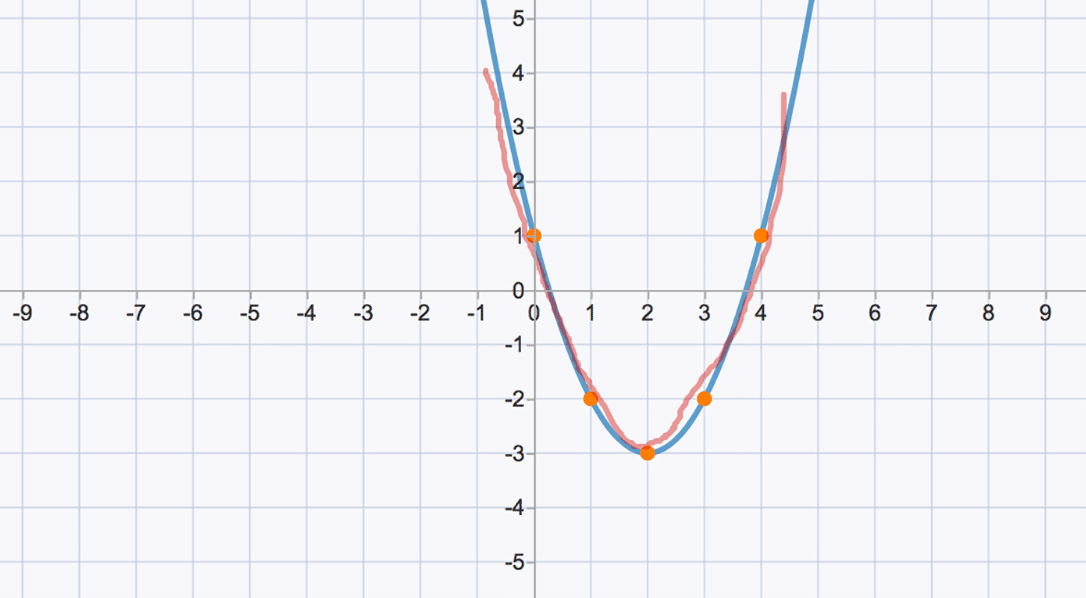
 Explanation y = x2 − 2x 8 or y = (x2 − 2x 1) −1 8 or y = (x − 1)2 7 Comparing with vertex form of equation f (x) = a(x −h)2 k;(h,k) being vertex we find here h = 1,k = 7,a = 1 ∴ Vertex is at (1,7) and vertex form of equation is y = (x − 1)2 7 graph {x^22x8 3554, 3558, 1778, 1778} Ans Answer linkThe quadratic formula gives two solutions, one when ± is addition and one when it is subtraction x^ {2}2xy8=0 x 2 2 x − y − 8 = 0 This equation is in standard form ax^ {2}bxc=0 Substitute 1 for a, 2 for b, and 8y for c in the quadratic formula, \frac {b±\sqrt {b^ {2}4ac}} {2a}Learn honors algebra 2 standard form vertex with free interactive flashcards Choose from 303 different sets of honors algebra 2 standard form vertex flashcards on Quizlet

7 1 Graphs Of Quadratic Functions In Vertex Form Pdf Free Download

Vertex Intercept And Standard Form Read Algebra Ck 12 Foundation

Free functions vertex calculator find function's vertex stepbystep This website uses cookies to ensure you get the best experience By using this website, you agree to our Cookie PolicyFinding the Vertex Form The required equation for an updown facing parabola is 4p(y−k) = (x−h)2 4 p ( y − k) = ( x − h) 2 and it has vertex (h,k) ( h, k) and the focal length p p InBut the equation for a parabola can also be written in "vertex form" y = a ( x − h) 2 k In this equation, the vertex of the parabola is the point ( h, k) You can see how this relates to the standard equation by multiplying it out y = a ( x − h) ( x − h) k y = a x 2 − 2 a h x a h 2 k This means that in the standard form, y

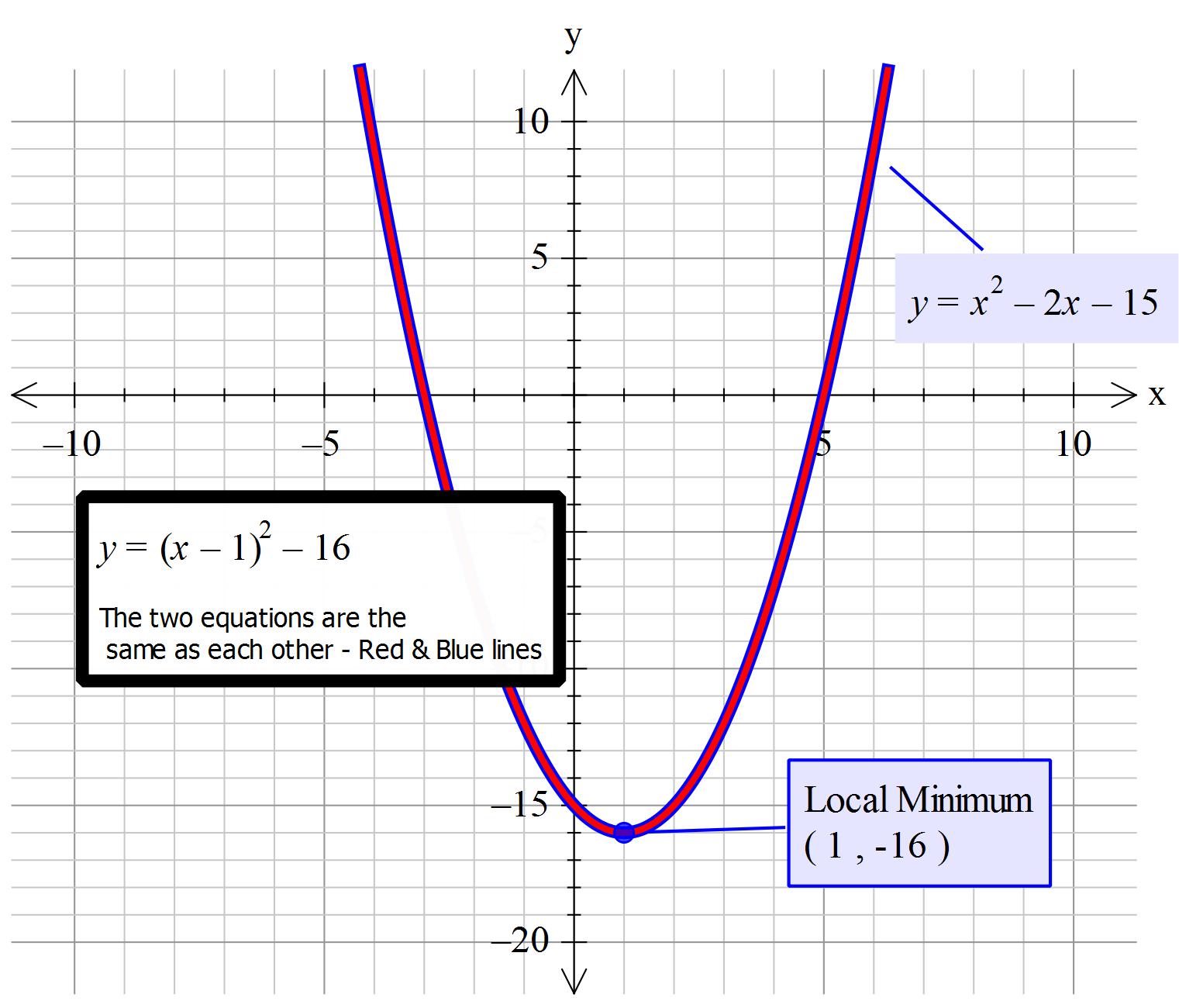
What Is The Vertex Form Of Y X 2 2x 15 Socratic

Complete The Square Lesson Ppt Download

Y = x2 − 2x − 8 y = x 2 2 x 8 Find the properties of the given parabola Tap for more steps Rewrite the equation in vertex form Tap for more steps Complete the square for x 2 − 2 x − 8 x 2 2 x 8 Tap for more steps Use the form a x 2 b x👉 Learn how to graph quadratic equations by completing the square A quadratic equation is an equation of the form y = ax^2 bx c, where a, b and c are cFind the Vertex f(x)=x^22x8 Rewrite the equation in term of and Rewrite the equation in vertex form Tap for more steps Complete the square for Substitute the values of , , and into the vertex form Set equal to the new right side Use the vertex form, , to determine the values of , ,

Find Factored Form And Vertex Of F X X 2 2x 8 Youtube

Mfg The Vertex Of A Parabola

Start with the given quadratic Subtract from both sides Factor out the leading coefficient This step is important since we want the coefficient to be 1 Take half of the x coefficient to get (ie )Find the Vertex y=1/2x^22x8 Rewrite the equation in vertex form Tap for more steps Combine and Complete the square for Tap for more steps Use the form , to find the values of , , and Consider the vertex form of a parabola Substitute the values of and into the formulaThe vertex of an equation in vertex form is (h,k), which for our equation is (6,4) Notes Right now our quadratic equation, y=x 2 12x32 is in standard form

Quadratic Functions

Write X 2 4x 3 In The Form Y X H 2 K Chegg Com

We want to get y = a (xh) k y = x 3x6 in the form Put brackets around the first two terms on the right, y = x 3x6 and since the coefficient of x is 1 put 1 in front of the parentheses Normally you would factor out the coefficient of x y = 1 xThis video screencast was created with Doceri on an iPad Doceri is free in the iTunes app store Learn more at http//wwwdocericomVertex Form Equation & Functions Just as y = mx b is a useful format for graphing linear functions, y = a(x h)^2 k is a useful format for graphing quadratic functions

Vertical Shifts Of Quadratic Functions Ck 12 Foundation

Exercises 2 3 In Problems 1 8 Find The Vertex Form Of Chegg Com

 Explanation Changing a quadratic function from standard form to vertex form actually requires that we go through the process of completing the square To do this, we need the x2 and x terms only on the right side of the equation y = x2 2x −8 y 8 = x2 2x −8 8 y 8 = x2 2x −8 8 y 8 = x2 2x** y=x^(2)8x1 complete the square y=(x^28x16)116 y=(x4)^217 This is an equation of a parabola that opens upwards with vertex at (4,17) Its standard form of equationy= (xh)^2k, (h,k) =(x,y) coordinates of the vertexWhat is y=x^(2)8x1 in vertex form?

Graphing Quadratic Functions

How To Graph A Quadratic Equation 10 Steps With Pictures

Divide 0 0 by − 8 8 Multiply − 1 1 by 0 0 Add 8 8 and 0 0 Substitute the values of a a, d d, and e e into the vertex form a ( x d) 2 e a ( x d) 2 e Set y y equal to the new right side Use the vertex form, y = a(x−h)2 k y = a ( x h) 2 k, to determine the values of a a, h h, and k k To change the expression (x2 2x) into a perfect square trinomial add (half the x coefficient)² to each side of the expression Here x coefficient = 2 So, (half the x coefficient)2 = (2/2)2 = 1 Add and subtract 1 to the expression The vertex form of the parabola with vertex (h, k) and axis of symmetry x = h is y = a (x h)2 k Find the vertex of the function y = –x2 2x 8 It is where the derivative 2x 2 = 0 Since you probably haven't learned about derivatives, do it this way Rewrite is as x^2 2x 8 = (x1)^2 7 Now look at the form of the formula on the right It

Desmos

Graph The Quadratic Function Y X 2 2x 3 Vertex X Y Intercepts Symmetry Domain Range Youtube

 Convert equation from quadratic form to vertex form, y= a(xh)^2 k, by completing the square y= 25x^255x525 math which form of a quadratic funtion is easiest to use to find the maximum or minimum value of the function? Complete the square to rewrite the quadratic function in vertex form y = x ^ 2 2x 8 Answers 3 Get Other questions on the subject Mathematics Mathematics, 1530, southerntouch103 Gretchen is setting up for a banquet she has 300 chairs and needs to distribute them evenly among t tables how many chairs should she put atAlgebra Find the Vertex Form y=x^22x8 y = x2 − 2x − 8 y = x 2 2 x 8 Complete the square for x2 −2x−8 x 2 2 x 8 Tap for more steps Use the form a x 2 b x c a x 2 b x c, to find the values of a a, b b, and c c a = 1, b = − 2, c = − 8 a = 1, b = 2, c =

2

Converting Quadratic Equations Worksheet Coach Forrester

Because of the symmetry of a parabola, the vertex is found on the vertical line exactly halfway between the roots, so x=3 (you can add the coordinates of the two roots and divide by 2, to find the midpoint of the segment between them) The y value at the vertex is y (3) = 2 (3 – 5) (3 – 1) = − 8 meaning the vertex has the coordinates (3, 8)Plug (1,7) into the equation and define b in terms of a math7=ab8\\b=a1/math (0,8) is a point on the parabola, so by symmetry, (2,8) is also a point Plug (2,8) into the equation and define b in terms of a math8=4a2b8\\b=2a\\/mathStart with y = x^2 8x 2 add 2 to both sides of the equation to get y 2 = x^2 8x complete the square on the expression on the right side of the equation to get y 2 = (x4)^2 16 subtract 2 from both sides of the equation to get y = (x4)^2 18 that's your vertex form

Quadratic Functions Examples Solutions Videos

Quadratics Review 1 Quadrtics Test Review 1

The two answers below are perfect;Create your account View this answer The given equation is y =x2−2x−8 y = x 2 − 2 x − 8 To convert this into the vertex form, we have to complete the squares Adding 8 8 on both sidesIn vertex form as 1) f(x) =(3x6)2 −25 2) f(x) =3(x6)2 −25 3) f(x) =3(x2)2 −1 4) f(x) =3(x2)2 7 5 Which equation is equivalent to y−34 =x(x−12)?

Biomath Quadratic Functions

Example 4 Write A Quadratic Function In Vertex Form Write In Vertex Form Then Identify The Vertex X 2x 2 10x 22 Y Solution X 2x 2 10x 22 Y Write Ppt Download

5 Write The Equation Of The Parabola In Vertex Form Chegg Com

Finding Features Of Quadratic Functions Video Khan Academy

Http Www Manhassetschools Org Cms Lib8 Ny Centricity Domain 710 Group work 59 63 solutions Pdf

Vertex Form Of Quadratic Functions Math 2 Y

Www Scasd Org Cms Lib Pa Centricity Domain 1229 2 2 a2 17 unit 2 2 ws packet lg Pdf

What Would An Equation For A Quadratic Function In Vertex Form With Vertex 1 6 That Passes Through The Point 3 4 Be Quora

Parabolas In Standard Intercept And Vertex Form Video Lesson Transcript Study Com

Y X 3 Graph

Quadratic Functions

Draw The Graph Of The Polynomial F X X 2 2x 8

View Question What Is The Vertex Of The Equation Y X 2 2x 8

Http Www Midwayisd Org Cms Lib Tx Centricity Domain 164 Preap alg ii 4 7b Pdf

Draw The Graph Of The Polynomial F X X 2 2x 8 Sarthaks Econnect Largest Online Education Community

Standard 9 Write A Quadratic Function In Vertex Form Ppt Video Online Download

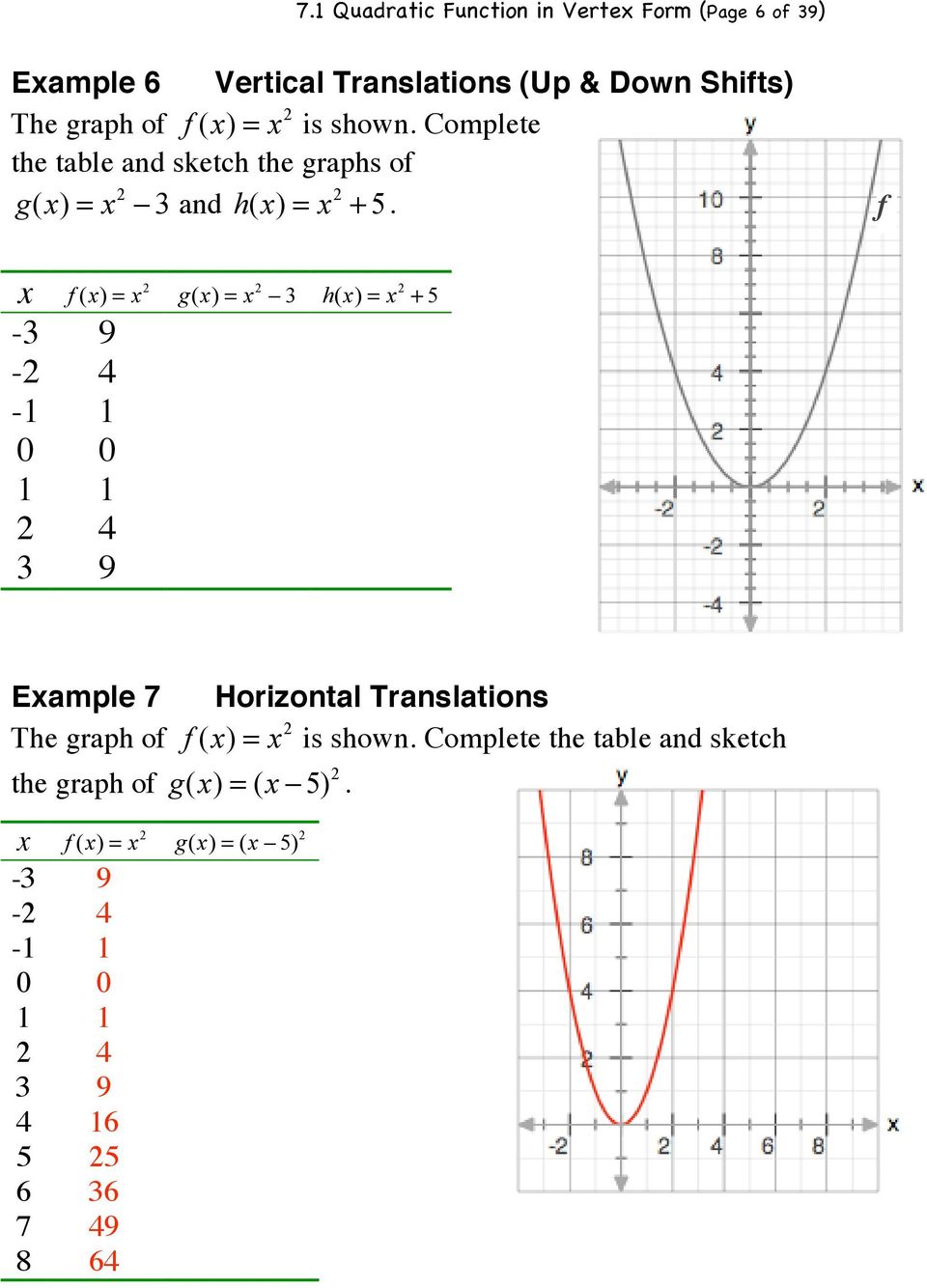
7 1 Graphs Of Quadratic Functions In Vertex Form Pdf Free Download

Graphing Parabolas In Vertex Form Worksheet Promotiontablecovers

Mfg Problem Solving

What Is The Axis Of Symmetry And Vertex For The Graph F X X 2 2x 8 Socratic

2 C U K2f0w1c2k Akduote

Vertex Form In 5 Minutes What Is Vertex Form How Do I Find It Mike S Calculators With Steps Free 21

6 3 Interpreting Vertex Form And Standard Form

Fireworks From Standard To Vertex Form Ppt Video Online Download

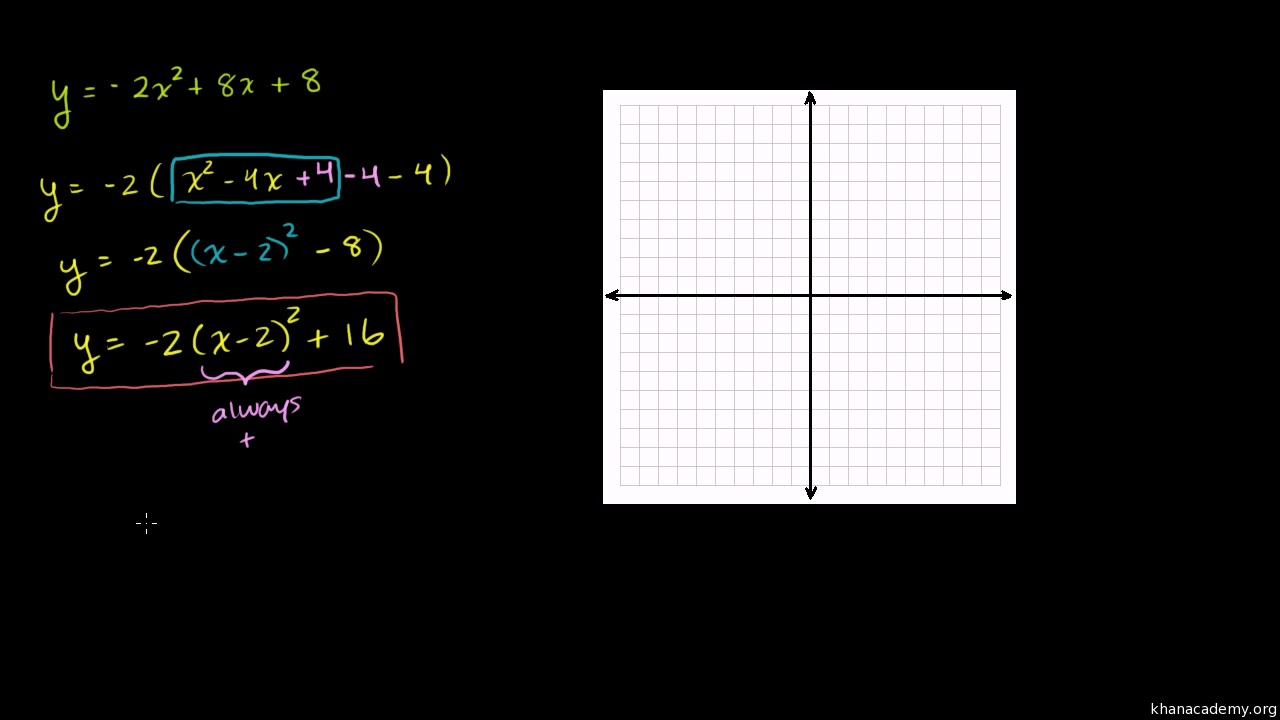
Vertex Axis Of Symmetry Of A Parabola Video Khan Academy

Vertex Form Of Quadratic Equation Mathbitsnotebook Ccss Math

Vertex Form In 5 Minutes What Is Vertex Form How Do I Find It Mike S Calculators With Steps Free 21

Changing Quadratic Functions From Standard Form To Vertex Form Flashcards Quizlet

Unit 8 Homework 3 Vertex Form Of A Quadratic Equation

Solve By Completing The Square X 2 2x 8 0 Solving Quadratic Equations Youtube

Chapter 5 Study Guide

Biomath Quadratic Functions

How To Graph Parabolas Krista King Math Online Math Tutor

Http Www Mrsfruge Com Uploads 1 2 0 0 P2a 3 3 Quadratic Functions Packet Pdf

What Is Vertex Form Example Get Education

Quadratic Equations And Quadratic Functions On The Sat

2

Completing The Square Vertex Form Of A Quadratic Expii

Converting Quadratic Equations Ppt Download

Sample Exam Grade 7

Converting A Quadratic Function From Standard Form To Vertex Form Completing The Square Youtube

2

How To Graph A Quadratic Equation 10 Steps With Pictures

Practice 1 2 Graphing In Vertex Form And Intercept Form

What Is The Vertex Form Of Y X 2 16x 71 With Steps Please Brainly Com

Untitled Document

Ppt Vertex Form Powerpoint Presentation Free Download Id

Given The Quadratic Yx22x 35 See How To Solve It At Qanda

The Vertex Form Of The Function Is Choose The Equation That Shows A Step In The Process Of Brainly Com

Characteristics Of Quadratic Functions Math 1 Eoct Review

Quadratic Equations And Quadratic Functions On The Sat

Vertex Form Vertex Form Vertex Form Is Another

Solved 1 1 1 Point What Is The Equivalent Vertex For Chegg Com

Rewriting Quadratics From Standard Form Into Vertex Form On Vimeo

7 1 Graphs Of Quadratic Functions In Vertex Form Quadratic Flip Ebook Pages 1 39 Anyflip Anyflip

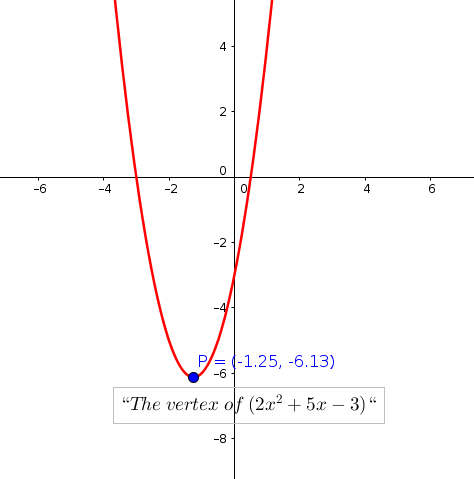
What Is The Vertex Form Of Y 2x 2 5x 3 Socratic

Solution Use The Graph Of Y X 2 2x 8 Does This Function Have A Maximum And Minimum And If So What Are They

4 1 Linear Applications Phone Charges The Monthly

Www K12northstar Org Cms Lib Ak Centricity Domain 4806 Alg1 quadratics packet blank Pdf

Graphing Parabolas

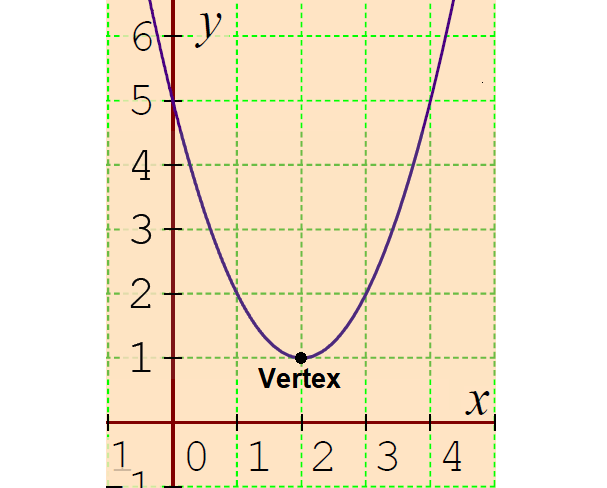
Vertex Form Of A Quadratic Equation

Solution Write Each Function In Vertex Form Sketch The Graph Of The Function And Label Its Vertex 33 Y X2 4x 7 34 Y X2 4x 1 35 Y 3x2 18x 36 Y 1 2x2 5x

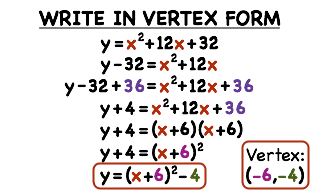
How Do You Convert A Quadratic From Standard Form To Vertex Form By Completing The Square Printable Summary Virtual Nerd

Http Www Tatecountyschools Org Userfiles 157 Classes 850 A3 review for test 3a Pdf Id

Ppt Converting Quadratic Equations Powerpoint Presentation Free Download Id

To Find The Vertex Transform The Quadratic Function From Standard Form To Vertex Form By Completing The Square Y 2x2 12x 10 2x2 6x 10 2x2 6x 9 18 10 2328 Square Meme On Awwmemes Com

Bingo Graphing Quadratics Parabolas In Vertex Form By Algebra Made Fun

Vertex Axis Of Symmetry Of A Parabola Video Khan Academy

7 1 Graphs Of Quadratic Functions In Vertex Form Quadratic Flip Ebook Pages 1 39 Anyflip Anyflip

Vertex Form Of Parabolas Kuta Software Form Of Vertex Form Of Parabolas Date Period Use Pdf Document

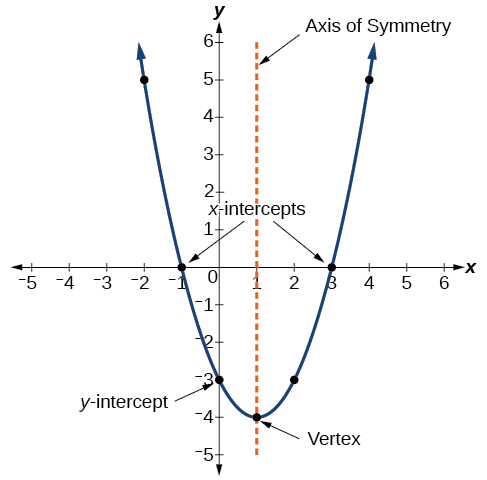
5 2 Quadratic Functions Mathematics Libretexts

1

2 2 Characteristics Of Quadratic Functions Flip Ebook Pages 1 10 Anyflip Anyflip

Transformations Of Quadratic Functions College Algebra

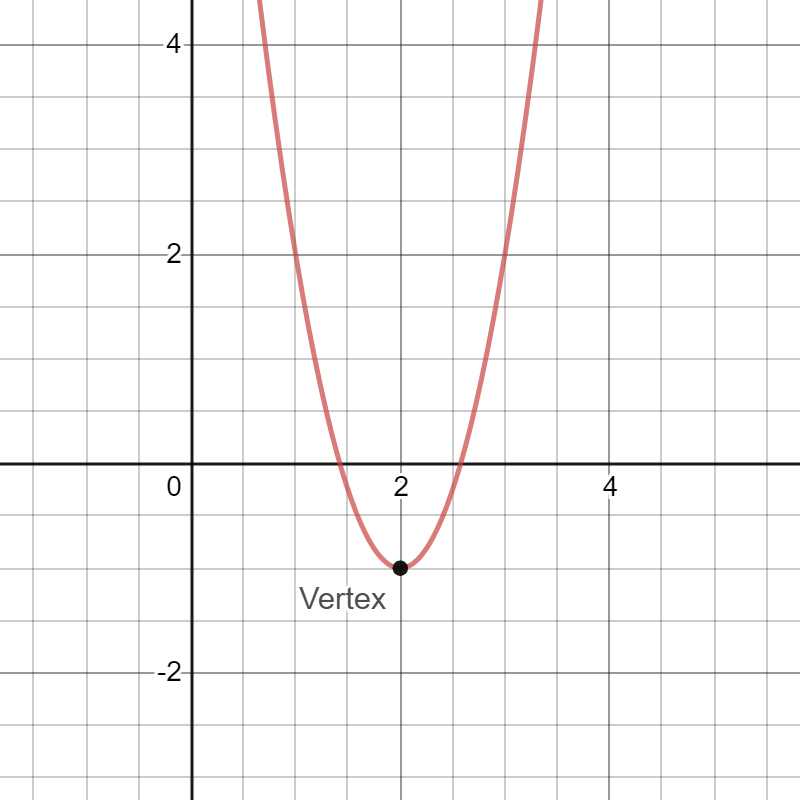
Forms Of Quadratics Explanations Tips And Examples Albert Resources

Answered C Complete The Table Sketch Each Bartleby

Incoming Term: y=x^2+2x-8 in vertex form,